SVD Subset Selection

Gene Golub and colleagues proposed a simple and, in our experience, too little known method for selecting a subset of well-conditioned columns from a badly conditioned or rank-deficient matrix. The method deserves to be better known.

Picking a few of the most linearly independent columns of a matrix is a hard problem in general. SVD subset selection is a simple heuristic method that picks a subset of k columns from a matrix that estimates the best-conditioned subset of columns of size k. The method works best when the matrix is rank-deficient and there is a clear indication of numerical rank (a gap in the singular values)—see the references [3,4] for more details. We find the method to work reasonably well with many ill-conditioned matrices. It does not do a great job of estimating the most linearly independent columns when the matrix is well-conditioned, but in that case the subset selection question is perhaps not the right one to ask about the data.

The method's R implementation shown below is short and sweet. It produces a set of column indices that estimate the k most linearly independent columns of the input matrix. 

# svdsubsel
#
# Input m*p matrix A, m >= p.
# Number of output columns k<=p.
# Returns an index subset of columns of A that *estimates* the k most linearly
# independent columns of A.

svdsubsel <- function(A,k=ncol(A))
{
  S <- svd(scale(A,center=FALSE,scale=TRUE), k)
  n <- which(svd(A)$d < 2*.Machine$double.eps)[1]
  if(!is.na(n) && k>=n)
  {
    k <- n - 1
    warning("k was reduced to match the rank of A")
  }
  Q <- qr( t(S$v[,1:k]) ,LAPACK=TRUE)
  sort(Q$pivot[1:k],decreasing=FALSE)
}
SVD subset selection works on a matrix in isolation, independently of other aspects of a larger problem that may only employ subset selection in one step, for example in generalized linear models (GLMs). Superior subset selection can be achieved by taking account of additional available information (information provided by the response vector, for example). In particular for the GLM case we recommend the glmnet[2] implementation of the elastic net method.

On the other hand, SVD subset selection's sole reliance on a data matrix can also be an advantage, for example in unsupervised machine learning applications.

Example

Let's illustrate the SVD subset selection method with a simple example.

We construct in the sample R program below an ill-conditioned 10 x 10 matrix that is numerically singular. We then use SVD subset selection to select three columns that we hope are as linearly independent as possible. We then compare that selection with all 120 possible three-column subsets that can be formed from the matrix. Our basis for comparison is the condition number of the three column submatrix computed by R's kappa function.

You can change the seed value to see the result for different random-valued matrices. Lower the exponent value to improve the matrix condition number (and reduce the effectiveness of the method). 

# Construct a badly conditioned 10x10 matrix
set.seed(5) # Change the seed for different examples...
exponent <- 2  # Lower the exponent to improve the matrix condition number...

U <- qr.Q(qr(matrix(rnorm(100),10)))
V <- qr.Q(qr(matrix(rnorm(100),10)))
d <- exp(-(1:10)^exponent)
# In particular, note that the method does not work as well for well-conditioned
# matrices (by making the exponent < 1 for example).
A <- U %*% (t(V) * d)

# Use SVD subset selection to pick three columns
idx <- svdsubsel(A,3)

# *All* possible 3-column subsets of A:
all <- combn(10,3)

# Which combinations were chosen by SVD subset selection?
idx <- which(apply(all,2, function(x) all(x==idx)))

# Finally, let's plot the logarithm of the condition numbers of all possible
# 3-column subsets of A and highlight the ones chosen by SVD subset selection:
condition_numbers <- apply(all, 2, function(i) log(kappa(A[,i])))
p <- order(condition_numbers)
# All the condition numbers:
plot(condition_numbers[p], xaxt='n',
     xlab='Subset (sorted by condition number of submatrix)',
     ylab='log(condition number)',
     main='Logarithm of condition numbers of all 3-column subsets of A')

# Higlight the SVD subset selection's condition number:
set <- which(p==idx)
points(set,condition_numbers[p[set]], col=4,pch=20)
l <- sprintf("SVD selection of columns %s.",paste(all[,idx],collapse=","))
legend("topleft",legend=l, fill=4, col=4, bty='n')
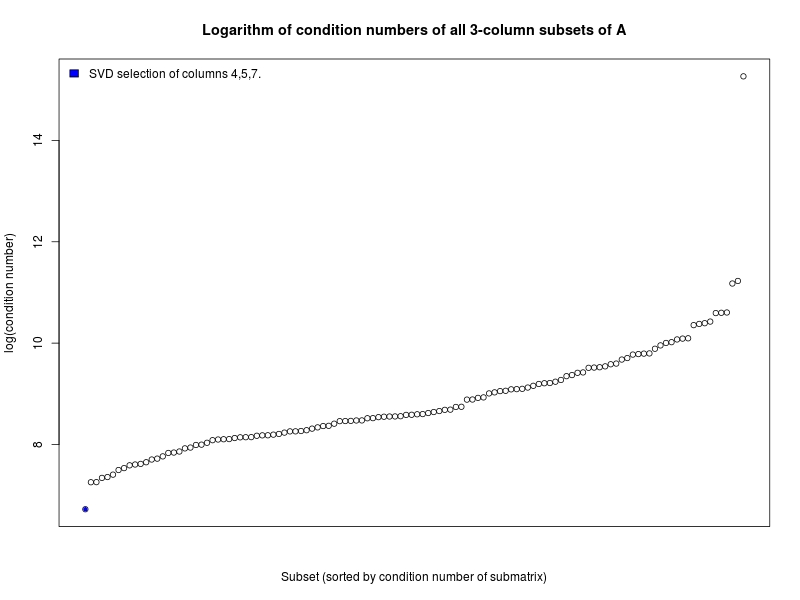
The example plots the condition numbers of all possible three-column submatrices from lowest to highest, and highlights and lists the selection made by the SVD subset selection method. The output typically looks like:
Submatrix condition numbers
The method selected the best conditioned three column submatrix in this example. It doesn't always pick the best answer, but generally works very well for rank-deficient and very ill-conditioned matrices.

Isn't the SVD computationally expensive for big problems?

Yes, that is indeed the case. But let's say that you're interested in a small well-conditioned subset of columns from a huge ill-conditioned matrix. No worries. In that case, we can use Baglama and Reichel's IRLBA method (and associated packages available for R, Python and Matlab) [1,5,6,7] to efficiently compute a truncated SVD.

References

  1. J. Baglama and L. Reichel, Augmented Implicitly Restarted Lanczos Bidiagonalization Methods, SIAM J. Sci. Comput. 2005.
  2. Jerome H. Friedman, Trevor Hastie, Rob Tibshirani, Regularization Paths for Generalized Linear Models via Coordinate Descent, JSS, Vol. 33, Issue 1, Feb 2010.
  3. Golub, G. Klema, V., Stewart, GW., Rank degeneracy and least squares problems, Technical Report TR-456, Department of Computer Science, University of Maryland, 1976.
  4. Golub, G. and Van Loan, C., Matrix Computations, 3ed., Johns Hopkins University Press, 1996, pp. 590--595.
  5. Matlab IRLBA package http://www.math.uri.edu/~jbaglama/software/irlba.m.
  6. Python IRLBA package https://github.com/bwlewis/irlbpy (also installable from pip).
  7. R IRLBA package http://cran.r-project.org/web/packages/irlba/index.html.

Copyright

Copyright (C) 2014 Michael Kane and Bryan W. Lewis

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the Github project files.